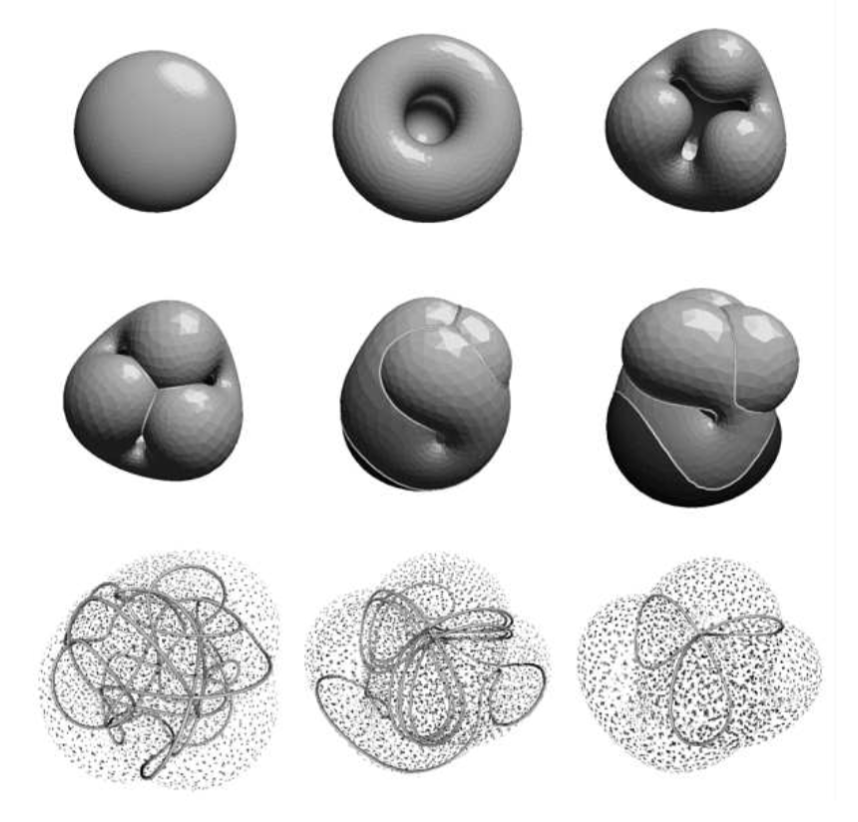
Primer

The history of this proof is an underdog story, the tale of the infamous Stephen F. Smale, before the glory of the Fields medal, when he was a struggling student in mathematics who prevailed against all expectation to prove the counter-intuitive fact that a sphere can be turned inside-out without cutting it.

We will build up your understanding of topology, the mathematics of the properties of shapes, and dive headfirst into advanced topics required to see the genius of the proof. It is an existence proof alone, meaning no procedure for the transformation is given. Nevertheless, the animated version will be highly motivating.

The sphere in question is not your average beach volleyball. It is strictly the mathematical object of a sphere, namely the sphere in three dimensions. Therefore, such a transformation would not be possible in the real world of atoms. The abstract sphere has properties the basketball does not. Chiefly, we can collapse a curve of the sphere under a movement of its points, a “transformation”, in which the curves intersect themselves. We can fold and stretch it infinitely in any direction, and still, prominent topologists in the early 20th century generally did not have a consensus that everting a sphere would be permissible unless a “cut” were made, allowing the inside surface to emerge fully as the outside became fully within.

To illustrate, we could simply cut a sphere in half, turn each half inside out, and attach the ends again to achieve an eversion. But how can it be done without cutting? That was a question that was burning to be solved in the 1950’s.

From the onset, one should realize that the proof will demonstrate that an ordinary sphere has a measurable property relating its “inside-outed-ness”. This property, astonishingly, turns out to be equal for the same sphere, turned inside out, under a smooth transformation. Therefore, the platonic sphere can be turned inside out without cutting it. If this does not boggle your mind, read no futher. The weeds be tall here.

Soft Introduction to Topology

Topology is a branch of mathematics that studies the properties of space that are preserved under continuous transformations. It’s like geometry, but instead of focusing on shapes and sizes, it looks at how spaces are connected and how they can be deformed. Imagine stretching, twisting, or bending objects without tearing or gluing them. Topologists are interested in what remains unchanged through these transformations.

The running joke is that a topologist cannot distinguish a coffee cup from a donut. Why? Abstractly, it is possible to transform one into the other by stretching and bending, but not tearing or cutting. Both have one hole, so they are topologically equivalent. By contrast a sphere and a donut are not topologically equivalent. One cannot produce a donut without cutting open a hole. Yet, a bowling ball and a sphere are equivalent. The finger-grips of the bowling ball can be smoothed out, yielding a plain sphere.

The Proof

The eversion involves the concept of regular homotopy, which is a continuous deformation of one embedding of a manifold into another, such that at every stage of the deformation, the manifold is smoothly immersed in the ambient space

Smale showed that there exists a regular homotopy between the standard embedding of the 2-sphere S_2 in R_3 and its mirror image, such that at every intermediate stage, the sphere is still an immersion (i.e., it does not intersect itself). This means that there is a continuous path in the space of immersions from the standard embedding to the antipodal embedding, where the sphere is turned inside out.

The key insight of Smale’s proof is the use of the h-principle (h for homotopy), which allows one to extend homotopies of embeddings to homotopies of immersions. By applying this principle, Smale was able to construct a homotopy that demonstrates the eversion of the sphere.